Generally, I like Adamchik's paper. The most interesting proposition is Proposition 1 which Adamchik attributes to G. Almkvist and A. Meurman. The proofs for Adamchik's Proposition 3, Proposition 5, and Proposition 6 are more drawn out and tortured than necessary. My theorem below is proved in less space and generalizes half the propositions in Adamchik's paper. Definition of Two FunctionsDefinition.
Function
The following theorem generalizes Adamchik's Proposition 3, Proposition 5, and Proposition 6. Generalization of Adamchik's Propositions 3, 5, and 6Theorem.
where coefficients
Proof.
We get
Therefore,
Comment.
Adamchik's Proposition 4The proof for Adamchik's Proposition 4 can also be simpler: Theorem.
Proof.
References
The first reference is Victor Adamchik's paper. The other
|
|
|
Jun 10, 2005 - Generalization of Adamchik's Formulas
|
 This note (
This note (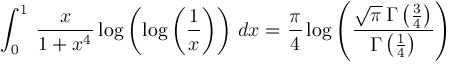
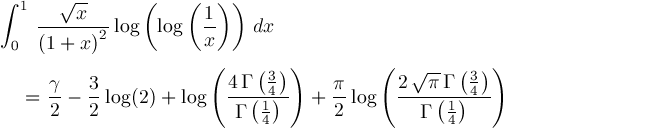
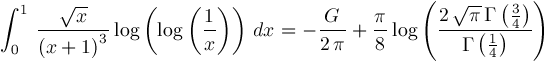
 For convenience, define
For convenience, define
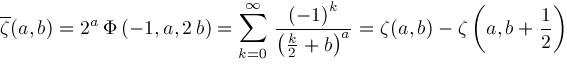
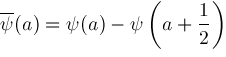
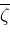 has properties
has properties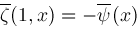
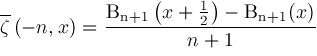
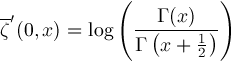
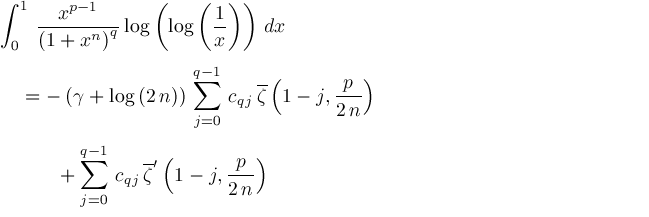
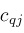 are determined by
are determined by
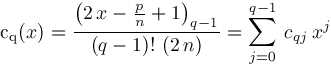
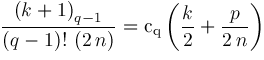
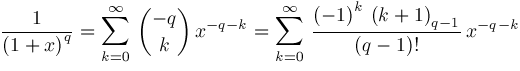
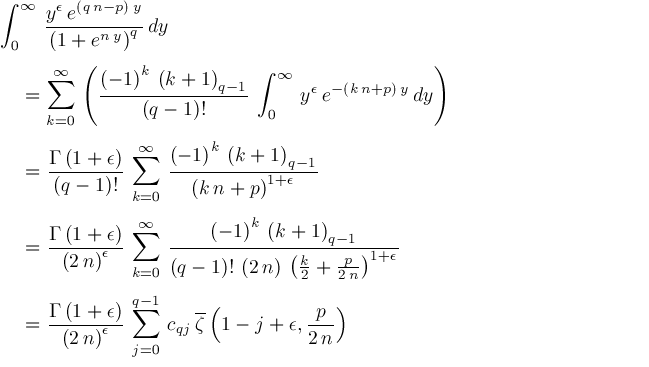
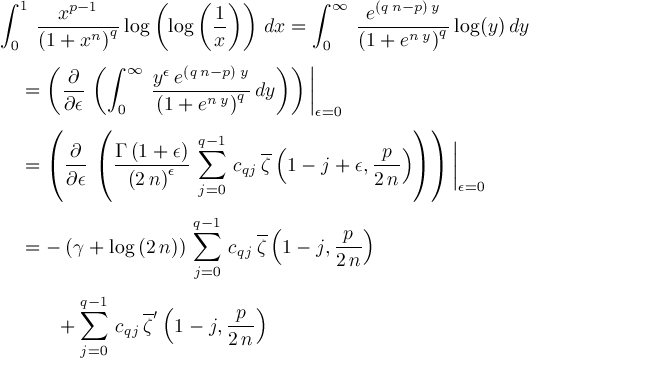
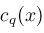 are
are
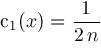
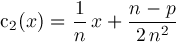
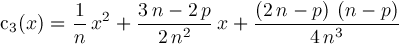
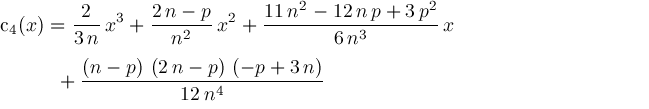
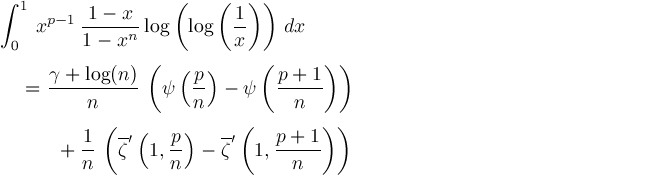
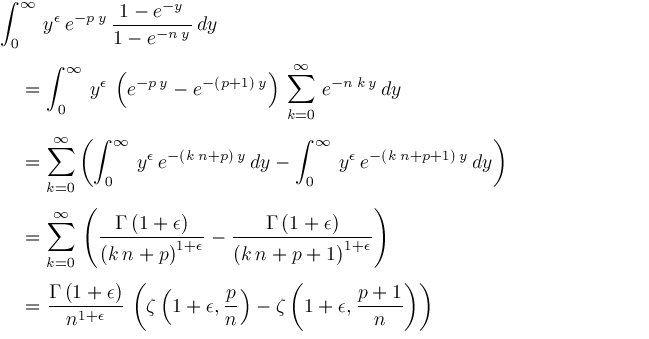
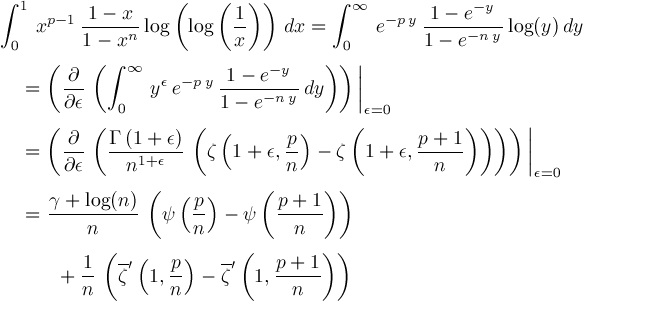
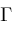 and
and
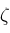 functions.
functions.