Hoenders and Slump[7]
describe a method for determining number and multiplicities of zeros of a function
based on a numerical quadrature technique, but as they show in their Tables 4-5, this
technique is unstable. It seems unlikely to us that any numerical technique
could decisively solve this problem. Symbolic methods can come to our aid in
some instances. First, if
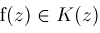 is a rational function over a suitable computable extension
is a rational function over a suitable computable extension
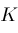 of
of
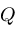 , then square-free factorization is applicable. Second, if , then square-free factorization is applicable. Second, if
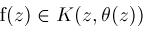 where
where
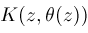 is a purely transcendental extension of a computable extension
is a purely transcendental extension of a computable extension
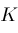 of
of
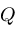 , ,
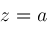 is a multiple zero, and
is a multiple zero, and
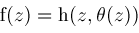 where
where
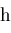 is a rational function, then
is a rational function, then
 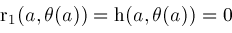
 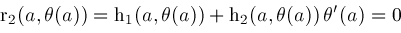
are rational functions in
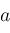 and
and
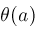 identical to zero. Since
identical to zero. Since
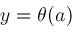 is a common root of both
is a common root of both
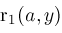 and
and
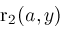 , the resultant , the resultant
 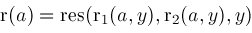
must be zero. Hence
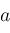 is a root of
is a root of
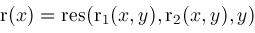 and is algebraic over
and is algebraic over
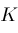 . The equation . The equation
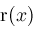 can be solved symbolically for
can be solved symbolically for
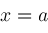 and then this solution substituted into
and then this solution substituted into
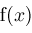 and
and
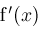 to ascertain if
to ascertain if
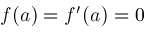 proving
proving
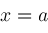 is a multiple zero. Third, if
is a multiple zero. Third, if
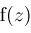 can be decomposed as a composition
can be decomposed as a composition
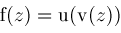 , ,
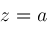 is a root of
is a root of
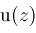 with multiplicity
with multiplicity
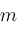 , ,
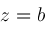 is a root of
is a root of
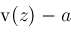 with multiplicity
with multiplicity
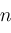 , then , then
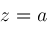 is a root of
is a root of
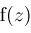 with multiplicity
with multiplicity
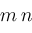 . .
A piecewise holomorphic function defined by
 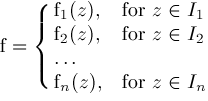
consisting of finitely many holomorphic
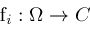 may be treated as
may be treated as
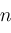 separate inputs to our algorithm.
separate inputs to our algorithm.
An expression
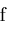 containing non-holomorphic subexpressions can sometimes be rewritten to become holomorphic
or piecewise holomorphic. As an example, suppose
containing non-holomorphic subexpressions can sometimes be rewritten to become holomorphic
or piecewise holomorphic. As an example, suppose
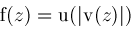 where
where
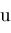 and
and
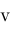 are holomorphic. Then solve
are holomorphic. Then solve
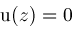 and replace
and replace
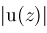 by better expressions
by better expressions
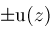 . .
Our algorithm is restricted to a finite interval
 . In some cases, such as . In some cases, such as
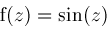 , this is necessary, for otherwise there would be an infinite number of solutions.
In other cases, such as , this is necessary, for otherwise there would be an infinite number of solutions.
In other cases, such as
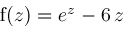 , there are only finitely many solutions even on , there are only finitely many solutions even on
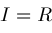 . The strategy proposed in this case is to use some asymptotic analysis to find . The strategy proposed in this case is to use some asymptotic analysis to find
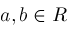 such that
such that
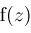 is non-zero on
is non-zero on
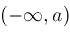 and
and
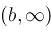 leaving only
leaving only
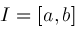 to contend with.
to contend with.
|
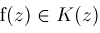 is a rational function over a suitable computable extension
is a rational function over a suitable computable extension
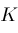 of
of
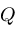 , then square-free factorization is applicable. Second, if
, then square-free factorization is applicable. Second, if
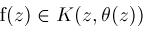 where
where
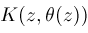 is a purely transcendental extension of a computable extension
is a purely transcendental extension of a computable extension
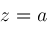 is a multiple zero, and
is a multiple zero, and
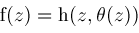 where
where
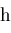 is a rational function, then
is a rational function, then
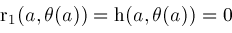
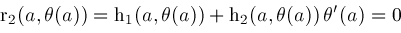
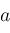 and
and
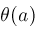 identical to zero. Since
identical to zero. Since
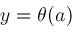 is a common root of both
is a common root of both
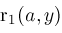 and
and
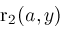 , the resultant
, the resultant
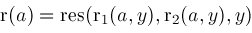
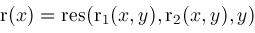 and is algebraic over
and is algebraic over
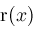 can be solved symbolically for
can be solved symbolically for
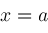 and then this solution substituted into
and then this solution substituted into
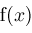 and
and
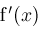 to ascertain if
to ascertain if
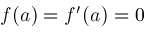 proving
proving
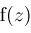 can be decomposed as a composition
can be decomposed as a composition
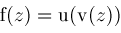 ,
,
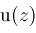 with multiplicity
with multiplicity
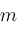 ,
,
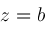 is a root of
is a root of
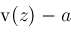 with multiplicity
with multiplicity
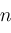 , then
, then
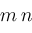 .
.
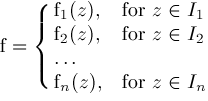
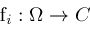 may be treated as
may be treated as
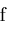 containing non-holomorphic subexpressions can sometimes be rewritten to become holomorphic
or piecewise holomorphic. As an example, suppose
containing non-holomorphic subexpressions can sometimes be rewritten to become holomorphic
or piecewise holomorphic. As an example, suppose
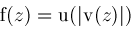 where
where
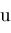 and
and
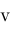 are holomorphic. Then solve
are holomorphic. Then solve
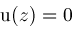 and replace
and replace
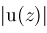 by better expressions
by better expressions
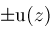 .
.
 . In some cases, such as
. In some cases, such as
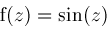 , this is necessary, for otherwise there would be an infinite number of solutions.
In other cases, such as
, this is necessary, for otherwise there would be an infinite number of solutions.
In other cases, such as
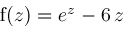 , there are only finitely many solutions even on
, there are only finitely many solutions even on
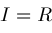 . The strategy proposed in this case is to use some asymptotic analysis to find
. The strategy proposed in this case is to use some asymptotic analysis to find
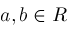 such that
such that
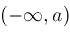 and
and
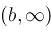 leaving only
leaving only
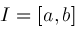 to contend with.
to contend with.