Bundy and Welham[3]
describe concepts of
attraction,
collection, and
isolation
which sometimes lead to solutions of nonlinear equations. Taking a somewhat
related algorithmic approach, suppose
where
For rule (1), let
For rule (2), let
Rules (1)-(2) are applied first. Rules (3)-(8) are applied with new factorization. This scheme will solve some equations. |
|
|
Elementary Solutions
|
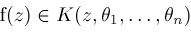 is an elementary expression where each
is an elementary expression where each
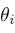 is exponential, logarithmic, or algebraic. Factoring, we suppose
is exponential, logarithmic, or algebraic. Factoring, we suppose
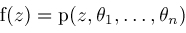 is irreducible in
is irreducible in
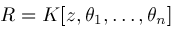 . Apply rules
. Apply rules
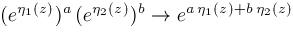
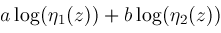
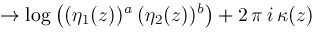
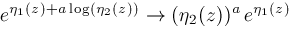
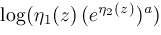
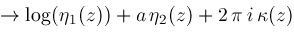
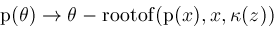
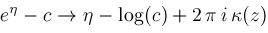
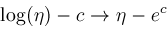
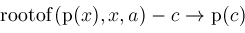
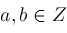 and
and
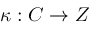 is an integer-valued piecewise constant function of
is an integer-valued piecewise constant function of
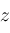 .
.
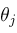 be exponentials. Try to find integers
be exponentials. Try to find integers
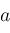 ,
,
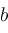 ,
,
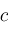 such that
such that
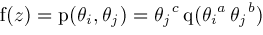 (consider
(consider
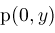 and degrees) and simplify
and degrees) and simplify
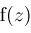 to
to
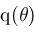 where
where
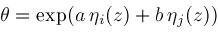 .
.
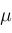 such that
such that
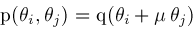 (consider
(consider
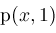 ,
,
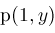 , and lcoeff's) and simplify
, and lcoeff's) and simplify
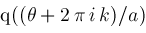 where
where
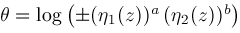 ,
,
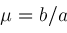 , and
, and
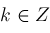 is chosen according to a given root
is chosen according to a given root
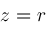 (given by our numerical algorithm).
(given by our numerical algorithm).