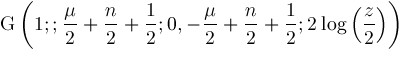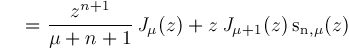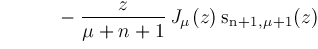Our previous paper "Hypergeometric Function Representations"
[15], presented an algorithm for computing formula representations of the hypergeometric
function
where we use notation
For example,
is a typical formula representation. Ability to compute such representations is applicable to integration, differential equations, closed form summation, and difference equations [7], [10], [13].
The Meijer G function,
However, not every
Our new algorithm computes formula representations such as
An ability to produce such representations is crucially important to the solution of hypergeometric type integrals which appear copiously in various integral tables [5], [11], [12], [13], used by scientists and mathematicians. In this paper, we repeat some familiar themes from our previous work [15], shift operators, contiguity relations, inverse shift operators, suitable origins, accessible origins, proper sequences, and lookup certificates but in a new and different context. Just the same, the current paper is completely self-contained and will stand on its own. |
|
|
Introduction
|
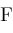 defined by
defined by

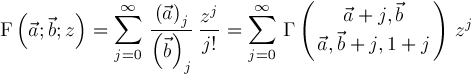
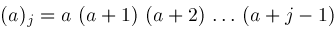
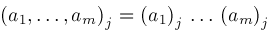
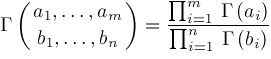
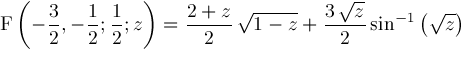
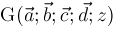 , defined in the next section, is a generalization of the hypergeometric function
, defined in the next section, is a generalization of the hypergeometric function
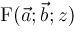 . Every hypergeometric function is a
. Every hypergeometric function is a
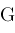 function:
function:
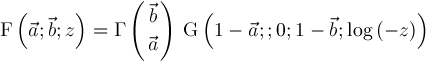
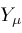 and
and
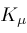 (
(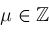 ), Kelvin functions
), Kelvin functions
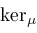 and
and
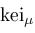 (
(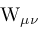 (
(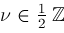 ), Lommel function
), Lommel function
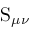 (
(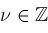 ), and Legendre function
), and Legendre function
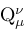 (
(