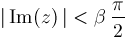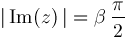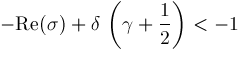We define the Meijer G function by the inverse Laplace transform
where
A schematic plot of the integration path
Contour
Related to this definition of Meijer G, we also define quantities
Analysis of the absolute convergence of the contour integral using Stirling's asymptotic formula for the gamma function produces:
Theorem.
Theorem.
Theorem. |
|
|
Definition
|

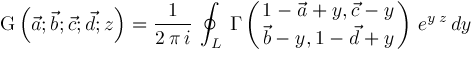
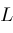 is one of three types of integration paths
is one of three types of integration paths
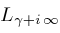 ,
,
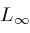 , and
, and
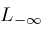 .
.
 ,
,
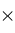 ) is shown below.
) is shown below.
 and finishes at
and finishes at
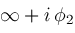 . Contour
. Contour
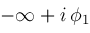 and finishes at
and finishes at
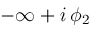 . Contour
. Contour
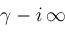 and finishes at
and finishes at
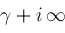 . All the paths
. All the paths
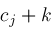 poles on the right and all other poles of the integrand (which must be of the form
poles on the right and all other poles of the integrand (which must be of the form
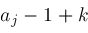 ) on the left. Define
) on the left. Define
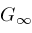 ,
,
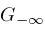 , and
, and
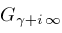 to be the
to be the
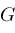 functions defined by the
functions defined by the
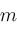 ,
,
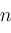 ,
,
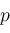 ,
,
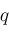 ,
,
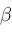 ,
,
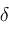 , and
, and
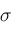 by
by
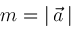 ,
,
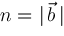 ,
,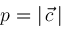 ,
,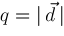 ,
,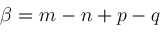 ,
,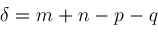 , and
, and
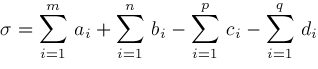

 converges absolutely if
converges absolutely if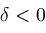
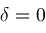
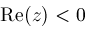
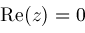 ,
,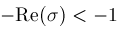
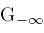 converges absolutely if
converges absolutely if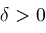
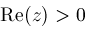
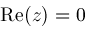 ,
,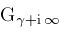 converges absolutely if
converges absolutely if