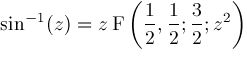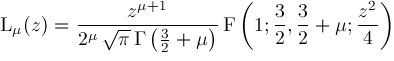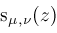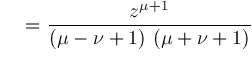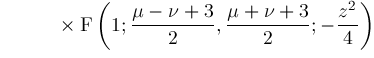The hypergeometric function
where
Various simple expressions and well known functions can be expressed in term of
hypergeometric functions are applicable to integration, differential equations, closed
form summation, and difference equations
[5],
[6],
[7]. Some methods will create answers in terms of
|
|
|
Introduction
|
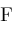 can be defined by
can be defined by

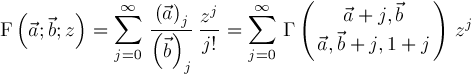
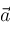 and
and
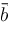 are vectors,
are vectors,
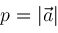 ,
,
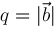 ,
,
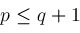 , and
, and
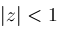 if
if
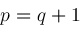 . Our objective is to compute representations for instances of
. Our objective is to compute representations for instances of
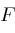 . For example,
. For example,
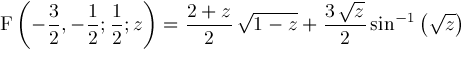
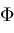 function
function