Let
presenting no further challenge to us.
We proceed to a
Also, the following contiguity relations are known:
Using these shift and contiguity relations, we can start from almost any
We show how to compute
Known:
Shift:
Contiguity:
Contiguity:
Shift:
Contiguity:
Shift:
Hence, we conclude:
This formula is not explicitly listed in [7]. Neither Mathematica 2.2 nor Maple 5.3 will compute it. Macsyma 419.0 does compute it, but returns a wrong answer.
We will develop a strategy using shift relations and contiguity relations for
|
|
|
2F1 Example
|
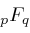 denote the restriction of
denote the restriction of
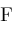 to
to
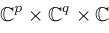 . Then
. Then
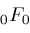 ,
,
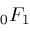 , and
, and
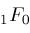 are representable by
are representable by

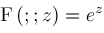
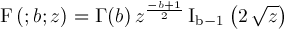
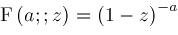
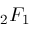 example which is more interesting. Let
example which is more interesting. Let
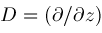 be the operator for differentiation. The following shift relations are known:
be the operator for differentiation. The following shift relations are known:
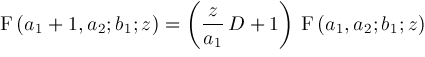
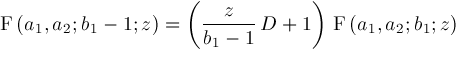
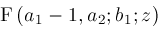
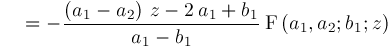
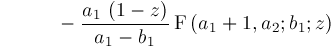
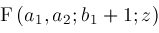
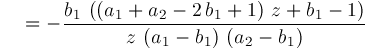
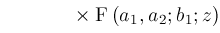
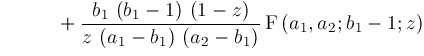
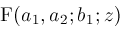 representation to obtain any
representation to obtain any
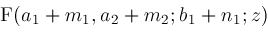 representation where
representation where
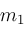 ,
,
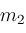 ,
,
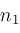
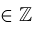 . The denominators appearing in the shift relations and contiguity relations
are troublesome since we can't let them become zero.
. The denominators appearing in the shift relations and contiguity relations
are troublesome since we can't let them become zero.
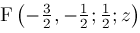 by starting from the known formula for
by starting from the known formula for
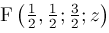 .
.
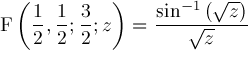
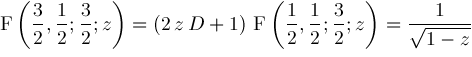
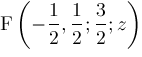
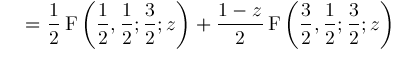
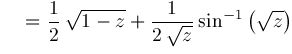
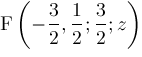
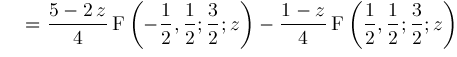
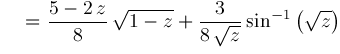
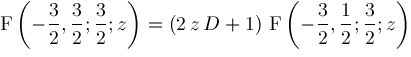
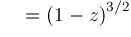
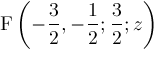
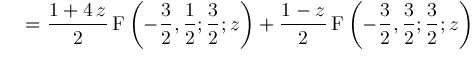
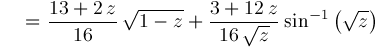
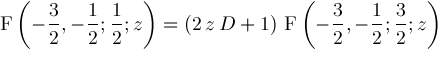
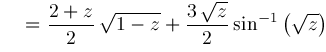
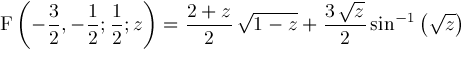
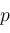 and
and
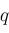 are arbitrary (subject to
are arbitrary (subject to
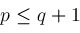 ) to compute
) to compute
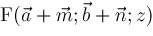 from
from
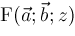 . First, we will study shift relations and contiguity relations for general
. First, we will study shift relations and contiguity relations for general