Let
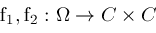 be holomorphic on
be holomorphic on
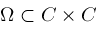 ; ;
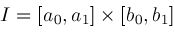 be a closed real parallelepiped contained in
be a closed real parallelepiped contained in
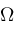 ; ;
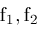 be real valued on
be real valued on
 ; curves ; curves
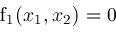 and
and
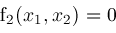 intersect in a finite number of points; the partial derivatives
intersect in a finite number of points; the partial derivatives
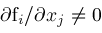 at each such point; the Jacobian
at each such point; the Jacobian
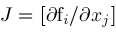 is nonsingular at each such point.
is nonsingular at each such point.
The two dimensional algorithm is like the one dimensional algorithm in that it uses
bisection. However in this case, bisection means cutting rectangles in half,
either widthwise or lengthwise depending on which way is most profitable in improving
precision. After each bisection,
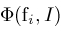 and
and
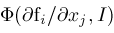 are computed. If
are computed. If
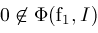 or
or
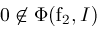 , then , then
 can be eliminated. Otherwise, continued bisection produces
can be eliminated. Otherwise, continued bisection produces
 such that
such that
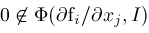 , in which case the extrema of , in which case the extrema of
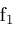 and
and
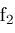 must occur at the corners of
must occur at the corners of
 . It is then possible to determine if . It is then possible to determine if
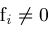 on some edge
on some edge
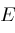 of
of
 and if so to use
and if so to use
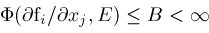 to perform narrowing.
to perform narrowing.
Bisection and narrowing ultimately produce a parallelepiped
 such that
such that
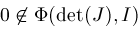 and both
and both
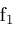 and
and
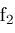 change sign on
change sign on
 . A nonsingular Jacobian . A nonsingular Jacobian
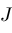 implies that
implies that
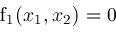 and
and
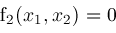 can intersect in at most one point
can intersect in at most one point
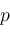 in
in
 . Each curve . Each curve
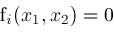 intersects the boundary
intersects the boundary
 of
of
 twice at points
twice at points
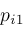 and
and
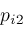 . Supposing . Supposing
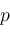 is in the interior of
is in the interior of
 , then all 4 intersection points , then all 4 intersection points
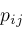 are distinct and can be isolated from each other. If the
are distinct and can be isolated from each other. If the
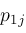 points alternate with the
points alternate with the
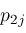 points around the perimeter of
points around the perimeter of
 , then the two curves actually do intersect and point , then the two curves actually do intersect and point
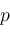 exists. Otherwise, the two curves do not intersect and
exists. Otherwise, the two curves do not intersect and
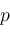 does not exist.
does not exist.
The generalization of Newton's formula to two dimensions is
 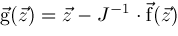
and bounds
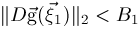 and
and
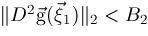 must be determined.
must be determined.
|
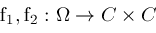 be holomorphic on
be holomorphic on
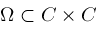 ;
;
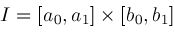 be a closed real parallelepiped contained in
be a closed real parallelepiped contained in
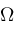 ;
;
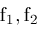 be real valued on
be real valued on
 ; curves
; curves
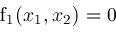 and
and
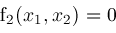 intersect in a finite number of points; the partial derivatives
intersect in a finite number of points; the partial derivatives
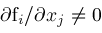 at each such point; the Jacobian
at each such point; the Jacobian
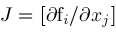 is nonsingular at each such point.
is nonsingular at each such point.
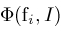 and
and
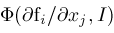 are computed. If
are computed. If
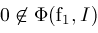 or
or
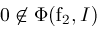 , then
, then
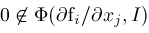 , in which case the extrema of
, in which case the extrema of
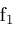 and
and
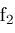 must occur at the corners of
must occur at the corners of
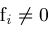 on some edge
on some edge
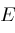 of
of
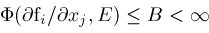 to perform narrowing.
to perform narrowing.
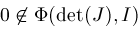 and both
and both
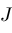 implies that
implies that
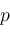 in
in
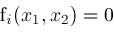 intersects the boundary
intersects the boundary
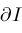 of
of
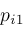 and
and
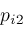 . Supposing
. Supposing
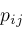 are distinct and can be isolated from each other. If the
are distinct and can be isolated from each other. If the
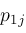 points alternate with the
points alternate with the
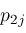 points around the perimeter of
points around the perimeter of
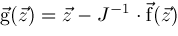
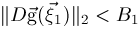 and
and
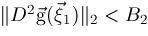 must be determined.
must be determined.