In this section we sketch ideas we have implemented to compute zeros of a smooth real-valued
function on a real interval. Let
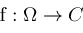 be holomorphic on
be holomorphic on
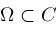 , ,
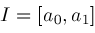 be a closed real interval contained in
be a closed real interval contained in
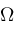 , ,
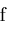 be real valued on
be real valued on
 , ,
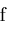 be not constant on
be not constant on
 , and , and
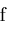 have simple zeros on
have simple zeros on
 . .
Since
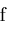 is holomorphic,
is holomorphic,
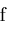 is infinitely differentiable. (Corollary 2.12, page 73, Conway[5]). Since
is infinitely differentiable. (Corollary 2.12, page 73, Conway[5]). Since
 is compact,
is compact,
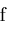 and
and
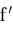 have finitely many zeros on
have finitely many zeros on
 . (Theorem 3.7, page 78, Conway[5]). The zeros of . (Theorem 3.7, page 78, Conway[5]). The zeros of
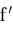 on
on
 are distinct from the zeros of
are distinct from the zeros of
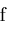 on
on
 because the zeros of
because the zeros of
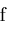 are simple. Therefore, recursively bisecting
are simple. Therefore, recursively bisecting
 into increasingly smaller subintervals eventually isolates each zero
into increasingly smaller subintervals eventually isolates each zero
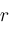 of
of
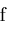 on
on
 in a subinterval
in a subinterval
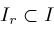 on which
on which
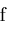 is also strictly monotone.
is also strictly monotone.
Now, we assume the existence of an interval arithmetic package
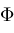 such that given any derivative
such that given any derivative
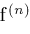 of
of
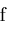 and subinterval
and subinterval
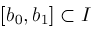 , we have , we have
 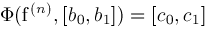
with either
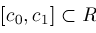 or
or
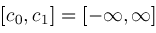 . Given any set . Given any set
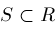 , define open neighborhoods , define open neighborhoods
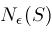 about
about
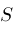 by
by
 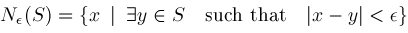
We let
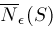 represent the closure of
represent the closure of
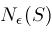 . .
We will assume
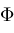 has the following continuity property: Given any
has the following continuity property: Given any
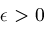 , ,
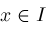 , and derivative , and derivative
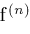 of
of
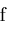 , there exists , there exists
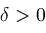 (
(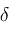 may depend on
may depend on
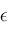 , ,
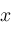 , and , and
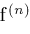 ) such that if ) such that if
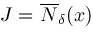 , then , then
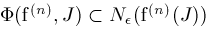 . In fact, by the compactness of . In fact, by the compactness of
 we can suppose
we can suppose
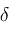 is independent of
is independent of
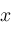 (see Rudin[14]).
(see Rudin[14]).
All of the above leads us to the following primitive algorithm for detecting zeros
of
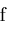 . .
proc
Zeros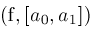
if not
CouldBeZero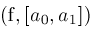 then
then
 return
return
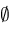 ; ;
elif not
CouldBeZero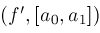 then
then
 if
if
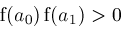 then
then

 return
return
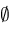 ; ;
 else
else

 return
Locate
return
Locate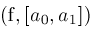 ; ;
 fi;
fi;
else

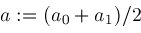 ; ;
 if
if
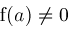 then
then

 return
Zeros
return
Zeros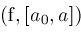
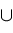 Zeros
Zeros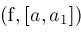 ; ;
 else
else


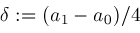 ; ;

 while
CouldBeZero
while
CouldBeZero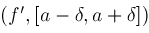 do
do



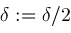 ; ;

 od;
od;

 return
Zeros
return
Zeros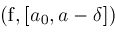
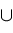
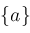



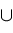 Zeros
Zeros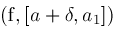 ; ;
 fi;
fi;
fi;
proc
CouldBeZero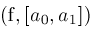
return
(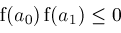 or
or
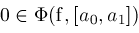 ); );
proc
Locate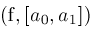
if
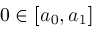 and
and
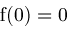 then
then
 return
return
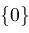 ; ;
else
 while true do
while true do


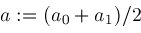 ; ;

 if
if
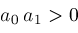


 and
and
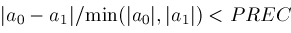 then
then


 break;
break;

 elif
elif
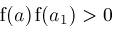 then
then



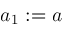 ; ;

 else
else



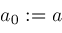 ; ;

 fi;
fi;
 od;
od;
 return
return
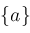 ; ;
fi;
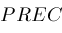 is a small positive number like
is a small positive number like
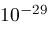 determined by the current working precision. The next two sections sketch ideas
that improve the time efficiency of this algorithm. The Mean-Value Theorem speeds
up procedure Zeros. Newton's method speeds up procedure Locate.
determined by the current working precision. The next two sections sketch ideas
that improve the time efficiency of this algorithm. The Mean-Value Theorem speeds
up procedure Zeros. Newton's method speeds up procedure Locate.
|
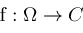 be holomorphic on
be holomorphic on
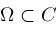 ,
,
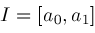 be a closed real interval contained in
be a closed real interval contained in
 ,
,
 be real valued on
be real valued on
 ,
,
 have finitely many zeros on
have finitely many zeros on
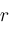 of
of
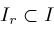 on which
on which
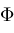 such that given any derivative
such that given any derivative
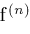 of
of
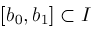 , we have
, we have
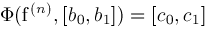
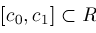 or
or
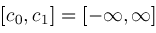 . Given any set
. Given any set
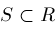 , define open neighborhoods
, define open neighborhoods
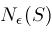 about
about
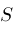 by
by
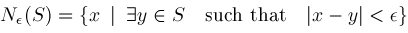
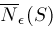 represent the closure of
represent the closure of
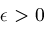 ,
,
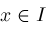 , and derivative
, and derivative
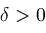 (
(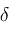 may depend on
may depend on
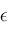 ,
,
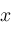 , and
, and
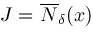 , then
, then
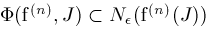 . In fact, by the compactness of
. In fact, by the compactness of
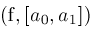
 return
return
 ;
; then
then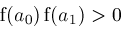 then
then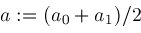 ;
;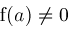 then
then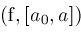
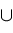 Zeros
Zeros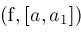 ;
;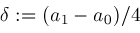 ;
;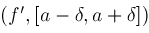 do
do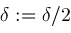 ;
;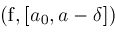
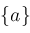
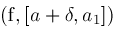 ;
;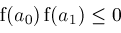 or
or
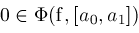 );
);
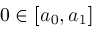 and
and
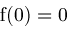 then
then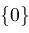 ;
;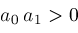
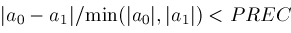 then
then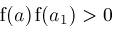 then
then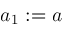 ;
;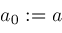 ;
;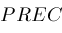 is a small positive number like
is a small positive number like
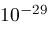 determined by the current working precision. The next two sections sketch ideas
that improve the time efficiency of this algorithm. The Mean-Value Theorem speeds
up procedure Zeros. Newton's method speeds up procedure Locate.
determined by the current working precision. The next two sections sketch ideas
that improve the time efficiency of this algorithm. The Mean-Value Theorem speeds
up procedure Zeros. Newton's method speeds up procedure Locate.