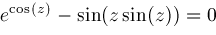Computer algebra systems such as Maple and Mathematica include numerical equation solvers such as fsolve and NSolve.  However, it seems that existing equation solvers are limited because they do not return all solutions and they are not guaranteed to find a solution if one exists.  Outside of polynomial systems, symbolic equation solving algorithms of such systems seem to be in even worse shape.  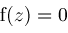Published numerical algorithms like Brent[2] start out with local assumptions about equations such as a change of sign in 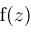has been detected and make it their goal to find a single root of .  Nerinckx and Haegemans[10] give a comparative study of 10 FORTRAN and ALGOL programs nonlinear equation solvers.  Rice[13] presents a slightly more up to date comparison of 8 nonlinear equation solvers. 

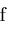We seek a more global approach which is guaranteed to find all solutions of an equation by assuming is holomorphic (a smooth function) and the domain 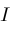of the unknown 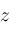is finite.  The last restriction is needed because Richardson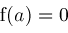[12] shows the problem is otherwise unsolvable.  We assume the zeros of are simple (meaning implies 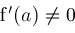), though we would like to lift this restriction.  Methods for escaping this restriction in some cases with multiple zeros (not simple) are discussed later. 

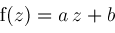Although "nonlinear equation" in general has a very broad meaning (see Saaty[15]), in this paper a nonlinear equation is an equation where is a univariate function that is not of the form .  Efficient algorithms for equations where is a polynomial in , such as Uspensky's algorithm or Sturm sequences are known and are described in Collins and Loos[4].  Our emphasis is on solving more difficult non-polynomial equations like

and at the same time offering a guarantee that we have found all the solutions.