Let
The differential equation for
Now
so
are defined if
If we express
which has degree
If we express
which has degree at most These results let us define
The coefficients of these polynomials in
Operators
|
|
|
Contiguity Relations
|

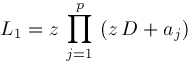
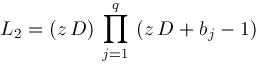
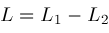
 becomes
becomes
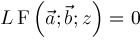
 is a polynomial in
is a polynomial in
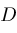 but
but
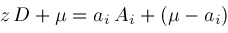
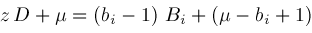
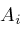 and
and
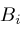 converting the differential equation
converting the differential equation
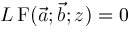 into a difference equation among contiguous instances of
into a difference equation among contiguous instances of
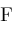 which we call a contiguity relation. Operators
which we call a contiguity relation. Operators
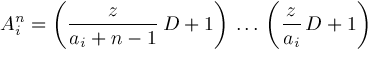
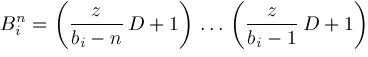
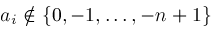 and
and
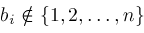 respectively.
respectively.
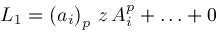
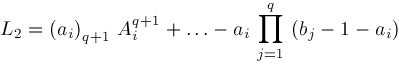
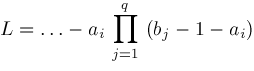
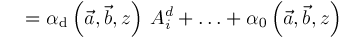
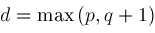 .
. 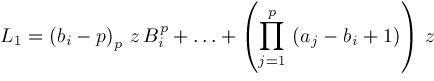
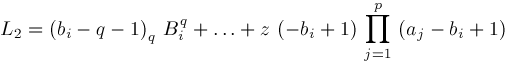
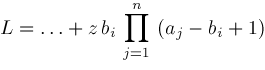
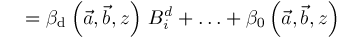
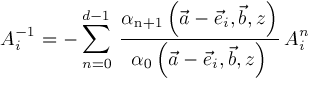
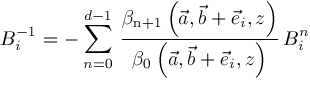
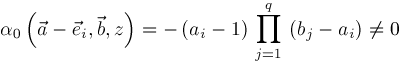
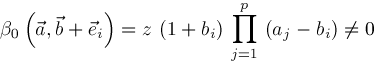
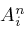 and
and
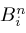 for
for
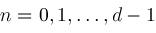 are defined if
are defined if
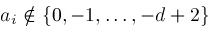 and
and
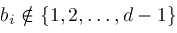 respectively. Hence,
respectively. Hence,
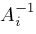 is defined if
is defined if
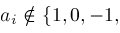
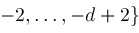 and
and
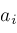 is distinct from all
is distinct from all
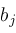 .
.
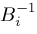 is defined if
is defined if
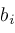 is distinct from all
is distinct from all
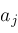 . Recall that
. Recall that