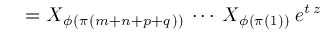Assume
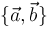 and
and
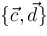 are disjoint. Suppose
are disjoint. Suppose
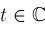 and
and
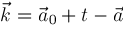 , ,
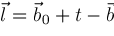 , ,
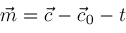 , ,
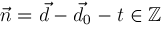 . We would try . We would try
 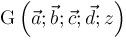
 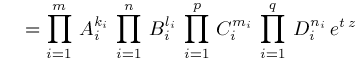
 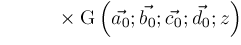
but this will not always work because of restrictions on where
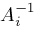 , ,
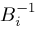 , ,
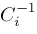 , and , and
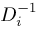 are defined.
are defined.
Given any vector
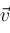 , let , let
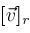 be the subvector of elements of
be the subvector of elements of
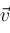 which are congruent to
which are congruent to
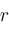 mod
mod
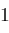 . Given any permutation . Given any permutation
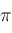 of
of
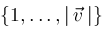 let
let
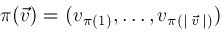 . .
Let
 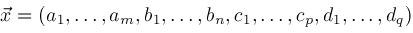
Let
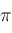 be a permutation which sorts
be a permutation which sorts
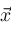 into nondescending order. Let
into nondescending order. Let
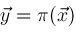 . Then . Then
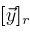 is nondescending for every
is nondescending for every
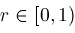 . .
Assume
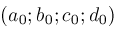 is a suitable origin such that
is a suitable origin such that
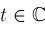 and
and
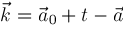 , ,
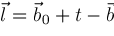 , ,
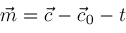 , ,
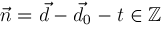 . Let . Let
 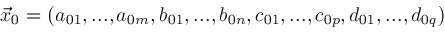
 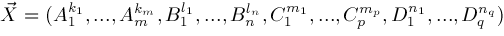
Let
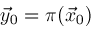 and
and
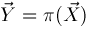 . Assume . Assume
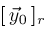 is nondescending for every
is nondescending for every
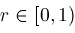 . .
For any given
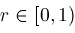 , plot the elements of , plot the elements of
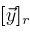 and
and
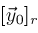 as a function of position. Call the resulting monotonic polygonal curves
as a function of position. Call the resulting monotonic polygonal curves
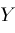 and
and
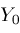 . For example, we might get this picture: . For example, we might get this picture:
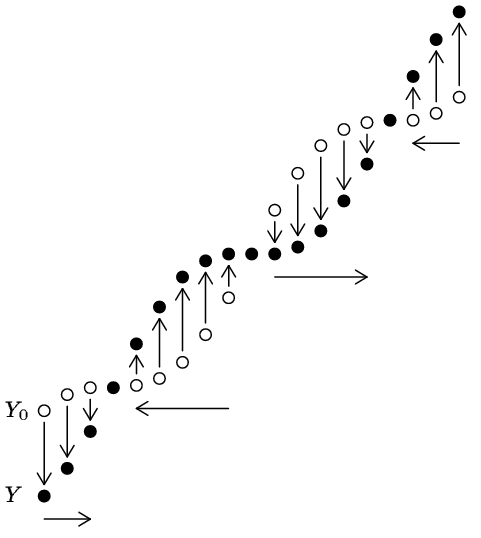
To avoid
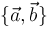 and
and
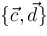 having elements in common as we apply
having elements in common as we apply
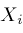 operators to
operators to
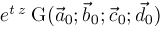 we may proceed left to right where
we may proceed left to right where
 lies below
lies below
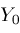 and right to left where
and right to left where
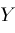 lies above or on
lies above or on
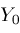 . .
Let
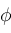 be a permutation of
be a permutation of
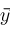 that in every plot of
that in every plot of
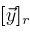 and
and
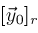 for every
for every
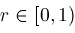 selects the elements of
selects the elements of
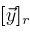 from left to right where
from left to right where
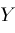 lies below
lies below
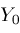 and selects the elements of
and selects the elements of
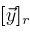 from right to left where
from right to left where
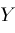 lies above or on
lies above or on
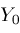 . Then we should apply . Then we should apply
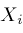 operators to
operators to
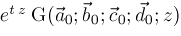 in the order
in the order
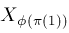 , ,
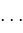 , ,
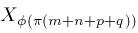 . That is, . That is,
 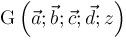
 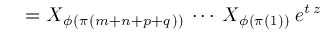
 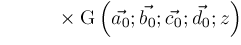
|
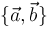 and
and
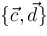 are disjoint. Suppose
are disjoint. Suppose
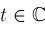 and
and
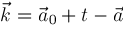 ,
,
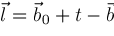 ,
,
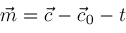 ,
,
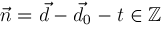 . We would try
. We would try

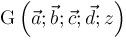
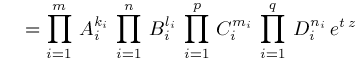
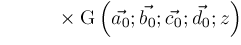
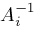 ,
,
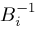 ,
,
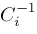 , and
, and
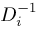 are defined.
are defined.
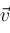 , let
, let
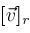 be the subvector of elements of
be the subvector of elements of
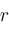 mod
mod
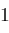 . Given any permutation
. Given any permutation
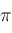 of
of
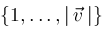 let
let
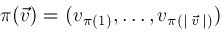 .
.
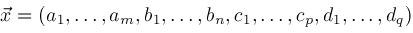
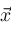 into nondescending order. Let
into nondescending order. Let
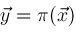 . Then
. Then
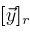 is nondescending for every
is nondescending for every
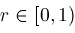 .
.
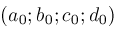 is a suitable origin such that
is a suitable origin such that
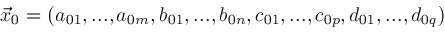
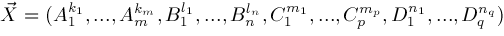
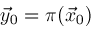 and
and
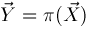 . Assume
. Assume
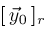 is nondescending for every
is nondescending for every
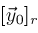 as a function of position. Call the resulting monotonic polygonal curves
as a function of position. Call the resulting monotonic polygonal curves
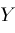 and
and
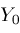 . For example, we might get this picture:
. For example, we might get this picture:

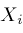 operators to
operators to
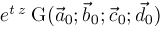 we may proceed left to right where
we may proceed left to right where
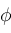 be a permutation of
be a permutation of
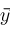 that in every plot of
that in every plot of
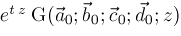 in the order
in the order
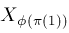 ,
,
 ,
,
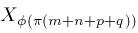 . That is,
. That is,