Operator
so
Let
where the
These results let us define
The coefficients of these polynomials in
Operators
are defined for all
|
|
|
Contiguity Relations
|
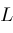 is a polynomial in
is a polynomial in
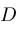 but
but

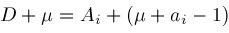
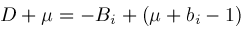
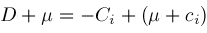
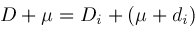
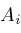 ,
,
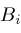 ,
,
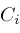 , and
, and
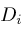 converting the differential equation for
converting the differential equation for
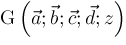 into a difference equation among contiguous instances of
into a difference equation among contiguous instances of
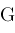 which we call a contiguity relation.
which we call a contiguity relation.
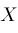 stand for
stand for
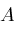 ,
,
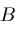 ,
,
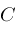 , or
, or
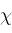 stand for
stand for
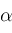 ,
,
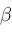 ,
,
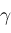 , or
, or
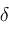 respectively. If we express
respectively. If we express
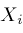 , then we get
, then we get
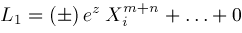
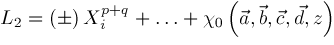
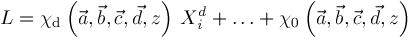
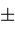 signs depend on
signs depend on
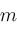 ,
,
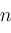 ,
,
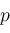 ,
,
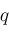 and whether
and whether
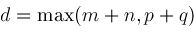 .
.
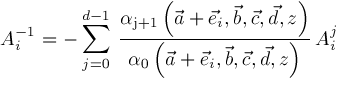
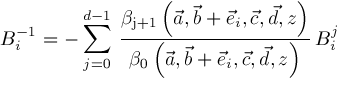
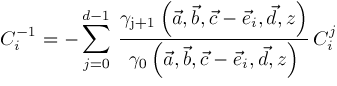
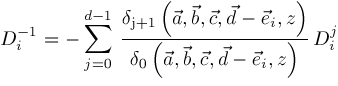
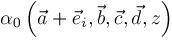
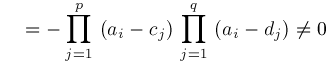
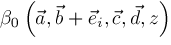
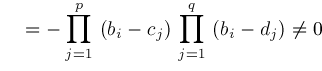
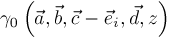
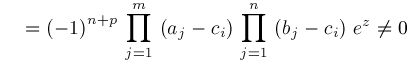
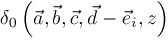
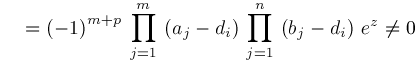
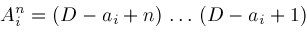
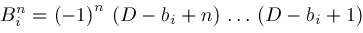
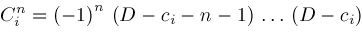
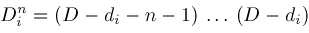
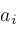 ,
,
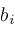 ,
,
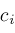 , and
, and
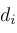 .
.