The main accomplishment of our algorithm is the essential reproduction of 1504 formulas
in 9 tables of representations of
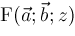 listed in
Integrals and Series, Volume 3: More Special Functions
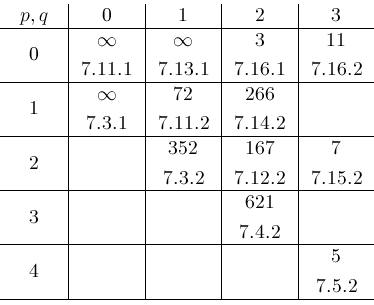
[7]. The total number of formulas in each of these tables is neatly summarized
by the following table:
listed in
Integrals and Series, Volume 3: More Special Functions
[7]. The total number of formulas in each of these tables is neatly summarized
by the following table:
The
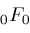 , ,
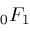 , and , and
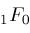 entries are covered by general formulas. The remaining 9 tables occupy most
of the 186 pages of Chapter 7 material on hypergeometric functions. Our algorithm
can be used to extend these tables to values of parameters very far out from those
given by
Integrals and Series, Volume 3: More Special Functions
[7]. The only limits on distance are the computer resources of time and memory.
entries are covered by general formulas. The remaining 9 tables occupy most
of the 186 pages of Chapter 7 material on hypergeometric functions. Our algorithm
can be used to extend these tables to values of parameters very far out from those
given by
Integrals and Series, Volume 3: More Special Functions
[7]. The only limits on distance are the computer resources of time and memory.
The next table indicates the proportion of
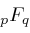 formulas with parameters in
formulas with parameters in
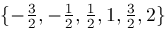 that can be reduced by our algorithm.
that can be reduced by our algorithm.
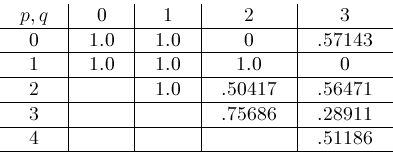
This table means, for example, that our algorithm was able to compute 51.186 of the
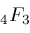 's. (Our algorithm does reduce other instances of 's. (Our algorithm does reduce other instances of
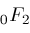 and
and
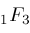 , but none with the parameters mentioned here.) , but none with the parameters mentioned here.)
In more recent work, our algorithm has been extended to compute representations for
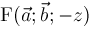 , therefore making our algorithm encompass even more elementary and special functions. , therefore making our algorithm encompass even more elementary and special functions.
|
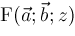 listed in
Integrals and Series, Volume 3: More Special Functions
listed in
Integrals and Series, Volume 3: More Special Functions

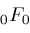 ,
,
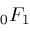 , and
, and
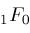 entries are covered by general formulas. The remaining 9 tables occupy most
of the 186 pages of Chapter 7 material on hypergeometric functions. Our algorithm
can be used to extend these tables to values of parameters very far out from those
given by
Integrals and Series, Volume 3: More Special Functions
entries are covered by general formulas. The remaining 9 tables occupy most
of the 186 pages of Chapter 7 material on hypergeometric functions. Our algorithm
can be used to extend these tables to values of parameters very far out from those
given by
Integrals and Series, Volume 3: More Special Functions
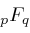 formulas with parameters in
formulas with parameters in
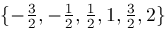 that can be reduced by our algorithm.
that can be reduced by our algorithm.

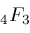 's. (Our algorithm does reduce other instances of
's. (Our algorithm does reduce other instances of
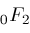 and
and
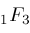 , but none with the parameters mentioned here.)
, but none with the parameters mentioned here.)
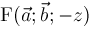 , therefore making our algorithm encompass even more elementary and special functions.
, therefore making our algorithm encompass even more elementary and special functions.