Once a root is sufficiently isolated by bisection and narrowing, a faster numerical method can be applied to obtain remaining digits of the root. Newton's method, the secant method, Muller's algorithm, third-order Newton iteration, and quadratic inverse interpolation all have superlinear convergence and are described in Rice[13]. We use Newton's method because it is well-known, is efficient, has low-overhead, and is easy to analyze.
Given function
If
Formulas for the derivatives of
Letting
for some
and we can guarantee that all
Now we assume
We modify procedure
Locate
and introduce procedures
NewtonTest
and
Newton. Procedure
NewtonTest
tests whether Newton's method should be used and procedure
Newton
actually implements Newton's method. These are listed below.
|
|
|
Newton's Method
|
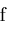 , define function
, define function
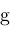 by
by
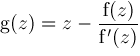
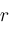 is a root of
is a root of
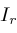 , then
, then
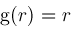 . Hence
. Hence
 . Newton's method for calculating root
. Newton's method for calculating root
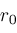 and then successively computes
and then successively computes
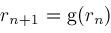 . Under the right conditions, explained below, the sequence
. Under the right conditions, explained below, the sequence
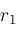 ,
,
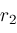 ,
,
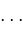 converges to
converges to
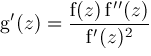
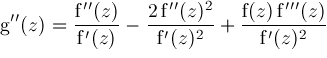
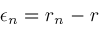 and using
and using
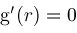 we obtain via Taylor series expansions the results
we obtain via Taylor series expansions the results
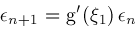
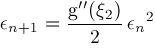
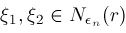 . If
. If
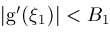 and
and
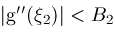 for all
for all
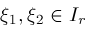 and
and
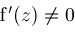 for all
for all
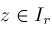 , then Newton's method is safe to use and converges faster than bisection if either
, then Newton's method is safe to use and converges faster than bisection if either
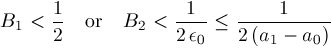
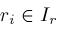 . The latter can be arranged by tweaking Newton's method so that if
. The latter can be arranged by tweaking Newton's method so that if
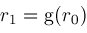 overshoots the boundaries of interval
overshoots the boundaries of interval
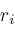 computed by
computed by
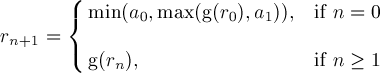
 's continuity property extends to derivatives
's continuity property extends to derivatives
 of
of
 . If interval
. If interval
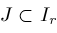 is sufficiently small, then
is sufficiently small, then
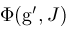 and
and
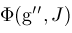 will determine finite bounds
will determine finite bounds
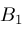 and
and
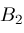 .
.
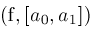
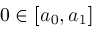 and
and
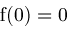 then
then return
return
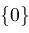 ;
;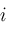 from
from
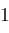 do
do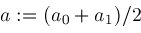 ;
;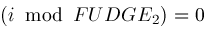
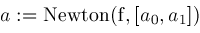 ;
;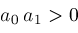
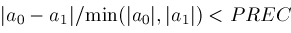 then
then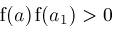 then
then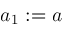 ;
;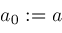 ;
;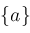 ;
;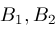 ;
;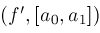 then
then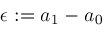 ;
;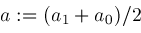 ;
;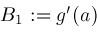 ;
;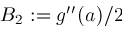 ;
;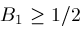 and
and
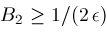 then
then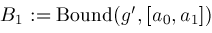 ;
;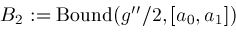 ;
;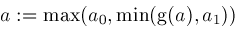 ;
;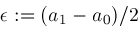 ;
;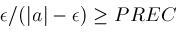 and
and
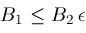 do
do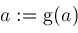 ;
;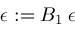 ;
;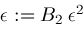 ;
; ;
; is another "fudge factor" which in our algorithm is currently set to the value
is another "fudge factor" which in our algorithm is currently set to the value
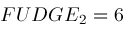 .
.